Annals of Marine Science
Effects of tidal wave modulation on coastal flooding along a tide-river context: Case of the seine estuary
EI Turki*, J Deloffre, R Gilbert, ET Mendoza, E Salameh, N Abcha, N Lecoq and B Laignel
Cite this as
Turki EI, Deloffre J, Gilbert R, Mendoza ET, Salameh E, et al. (2023) Effects of tidal wave modulation on coastal flooding along a tide-river context: Case of the seine estuary. Ann Mar Sci 7(1): 051-060. DOI: 10.17352/ams.000039Copyright License
© 2023 Turki EI, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.Tidal waves modulated over a range of timescales, from inter-daily to inter-annual variations, are responsible for coastal flooding which is enhanced in tide-river environments. The research described here investigates the tidal dynamics interacting with the fluvial component in the Seine estuary (NE France), an excellent natural laboratory for its time-varying flow and the available water-level records provided by tide gauges along the estuary. The tidal signal has been analyzed together with the river discharge during 25 years (1990-2015) in the Seine Bay, including the estuary and the marine tides at Cherbourg, by the use of a series of spectral and physical approaches. The main results highlighted that the tidal modulation is basically induced by the time changes of the harmonic components of M2, S2, N2, and K2 with significant shifts in the middle of the estuary. The estuary takes a flood-dominant behavior when the deformation of tides increases in the river section during the period 1999-2002 with an interaction between the high variability of tidal range and the extreme river discharge. This opposite effect of the river and its resistance is enhanced under higher tidal flow velocity; which increases the water depth and reduces the hydraulic head and the tidal amplification factor in a low turbid estuary.
This work carried out in the framework of the SWOT 3MC research program, gives some insights into the complex behavior of tidal propagation in the Seine estuary and its non-stationary dynamics close to the river effects in response to extreme sea levels leading to coastal flooding.
Introduction
Coasts and estuaries are dynamic areas of great economic and environmental importance related to the management of navigation channels and estuarine ecosystems [1,2] While coastal areas are open to oceans and exposed to marine forcing conditions involving a series of nearshore processes, estuaries are partially enclosed areas and subject to the physical interaction of driving forces (freshwater discharge, tides, and storm surges) with the effects of shallow water friction and basin topography [3-5]. This interaction of forces is mutually changing in accordance with the timescales from seasonal to inter-annual scales and is strongly enhanced in the global context of climate change including the sea level rise and the increase in the frequency of extreme events (e.g. fluvial floods, storm surges) leading to a higher occurrence of concomitance events and coastal flooding [6].
Understanding this complex interaction in estuaries, operating at different timescales is strongly required for improving the permanent operability of these systems and assessing the flood risks, particularly in environments largely influenced by anthropogenic factors (e.g. dams, harbors, navigation channels). The physical models, developed for estimating the water level in tide-river environments, are yet to be improved since their applicability is limited to reproducing the modulation effects of river discharge and the complexities induced by fluvial and marine oscillations, responsible for flood events. Furthermore, the riverine activity exhibits a strong nonlinear interaction with tidal waves that contributes to complex variations of water levels [4,7]. Indeed, tides are impinging from oceans to coasts and estuaries and would be nonlinearly modified by a series of physical factors related to the bed stress, topographic funneling of tides, wave incidence [8], and river frictional damping; a high river discharge enhances the friction of tides and their energy attenuation [4,9-11]. Such factors are generally balanced to modify the amplitudes of the principal harmonic constituents of tides and generate nonlinear frequencies responsible for their modification [7].
The tidal waves in estuaries are continuously inducing changes in tidal asymmetry because the propagation velocity varies with variations in water level. This amplification and deformation of the tidal wave in an estuary are directly related to the internal characteristics (morphology, hydraulic drag, etc.) of an estuary [12,13]. The development of tidal amplification and deformation, determined along the estuary by analyzing the water level data at different locations, thus gives insight into the hydrodynamics, including the compound flooding, and the morphological development as well.
In the framework of the SWOT 3MC program aiming to identify the contribution of the new SWOT mission in the calculation of tidal propagation of the Seine estuary (NE France), a series of preliminary scientific actions have been addressed to understand the non-stationary behavior of tides operating at different timescales between fluvial systems and marine environments. With the aim to investigate the effects of modulating tides on the coastal flooding in the Seine estuary, preliminary work has been performed to determine the time-variation of tidal deformation within the estuary, including the tidal amplification, the asymmetry and the hydraulic head, closer to the river discharge during the period 1990-2015. Here, our methodology uses a coupling of different techniques of wavelet spectral analysis and empirical methods, based on a physical approach similar but not identical to the method used by Wang, et al. [12], of estuarine tides in comparison with the marine tides of Cherbourg where tidal deformation is negligible.
Data and methods
Study site and database description
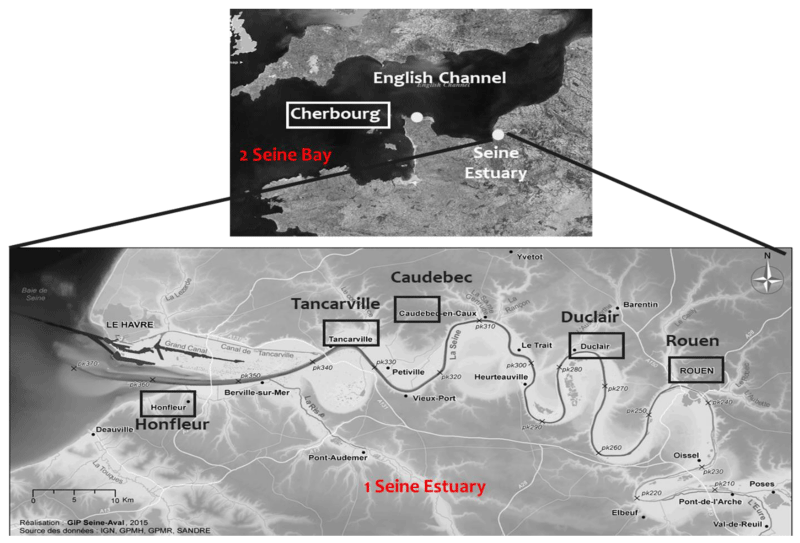
The Seine estuary is a river-tide system situated in the southern central English Channel (France). It exposes high spatial variations of tidal energy; the maximum tidal range is 8 m in the lower estuary (downstream, close to the marine part). This energy is combined with fluvial activity with a mean river discharge of ~ 435 m3/s and reaches a maximum of 903 m3/s during events of floods. Several anthropogenic activities in the estuary have been carried out since the middle of the 19th century and during the last two centuries [14]. The construction of new dykes induced significant changes in the bathymetry, by the increasing muddy facies, and then the water circulation system. [15,16]. This situation was balanced by the increase in mixed material, sandy mud, and muddy sand; there has been also a clear westward extension of muddy sand.
A series of tide gauges are deployed along 170 km, from the upper to the lower estuary, to provide a time series of hourly water levels. This is useful for understanding the estuarine dynamics and improving the calibrations of the numerical models. In this research, six records of 25-year hourly water levels (between 1990 and 2015) have been selected: five tide gauges along the Seine estuary (Rouen, Duclair, Caudebec, Tancarville, and Honfleur positioned respectively from the upper to the down estuary); a marine station at Cherbourg. The last station Cherbourg was taken as a reference in this study where the variability is fully controlled by marine effects and the tidal signal is not modified by the bottom effects (Figure 1).
Methods
Extraction of the tidal signal
In estuaries and tidal rivers, the signal of the total water levels is mainly governed by astronomical tides, river discharges, and surges; the last two forces continuously interacting with tides. The influence of shallow water friction and basin topography (estuarine length and convergence in width and depth) is modulating the total signal of water level along the estuary exhibiting a complex behavior explained by combining effects of 1) long-term trends; 2) astronomical tidal components; 3) effects of tidal wave deformation, 4) time-varying river discharges inducing strong nonstationary behavior in water level, 5) marine surges highly observed in the lower-estuary.
The most widely used methods for extracting the tidal signal are reported by the Classical Harmonic Analyses (CHA) which determine the amplitude and phase of a given frequency derived from astronomical and hydrodynamic theory. This method takes the following assumptions: 1) The stationary behavior of tides and their independence from other atmospheric and oceanic influences, 2) The independency between the different harmonic components, and 3) The fixed number of harmonic components with periodicities, phase angles, and amplitudes.
Using CHA, the tidal signal has been modeled as the sum of a finite set of sinusoids at specific frequencies to determine the sinusoidal phase/amplitude fitted to 18.61-, 9.305-, 8.85-, and 4.425-year sinusoidal signals [17]. This approach aims to predict the astronomical component of tides and obtain a quantitative assessment of the non-tidal component by simulating year-by-year the tidal constituents [18].
The radiational effects have been also considered for the extraction of the stochastic component from the water level signal [19].
In this research, the implemented hypothesis states the stationary dynamics of tidal waves in coastal and estuarine environments; which will be discussed further in the last section.
Indeed, the CHA is usually used in deep waters where the stationary assumption is valid for calculating the oceanic tides. This approach has been also used in various works to estimate coastal tides assuming their stationary behavior. For river-tide environments, the application of the CHA provides a non-tidal component including the effects of river discharges and surge signals as well as the nonstationary interactions of tides with meteorological forcing and fluvial flows. It can contain also the frequencies related to the energy from major constituents to their neighboring frequencies [20].
Wavelet spectral analyses
In the domains of hydrology, geophysics, and environmental sciences, the decomposition of the variability in a time-frequency or time scale is generally performed by the use of the Continuous Wavelet Transform [21-23]. This technique assumes that the signal is defined as the Gaussian derivative and correlated with a set of ‘daughter wavelets’ which are obtained by translation and dilation of a reference (the so-called ‘mother’) wavelet.
The continuous wavelet transform uses the Morlet wavelet (a Gaussian modulated sine wave) to offer a good basic frequency resolution, a wave number (~ 6 was used) for the reference mother wavelet resolution, and a good trade-off between spectral component detection and time localization.
The convolution of the signal in the wavelet transform is processed in Fourier space, hence replacing convolution with a simple algebraic product, and transforming the data back to the time domain to obtain the wavelet coefficients. However, the Fourier transform implies the occurrence of errors near the edge of the signal since it is not cyclic and of finite length. In the aim of avoiding this effect, zeroes can be usually added at the end of the signal, at the cost of a loss in power in the wavelet spectrum (the predicted power is underestimated as more zeroes are accounted for in the convolution process). More explanations are illustrated in Torrence and Compo’s [23] works.
Methodological approach for determining tidal wave deformation
With the aim to investigate the modification of the tidal wave along the Seine estuary, the tidal deformation from the upper to the lower zone has been analyzed. The deformation of the tidal wave should be related to the changes in its propagation velocity with the water level variation and its asymmetry. According to the previous works [1,12,13], the tidal modification along the estuary is strongly related to the physical characteristics of the estuary (morphology, water level slope, etc).
The development of the tidal deformation can be determined by analyzing the water level time series at the different stations to give some insights into the physical conditions of the estuary and their changes in time.
Our main motivation is to characterize the hydrodynamic regime along the estuary and its shift induced simultaneously by time changes in tidal deformation and river discharge. Such shift, related to the flooding would be associated with the non-linear interaction between the tidal wave propagation and the morphodynamics of the bottom and the suspended materials.
To do it, we have applied a conceptual approach to the hourly water levels at each station of the estuary (Rouen, Duclair, Caudebec, Tancarville, and Honfleur) with the aim to quantify changes in tidal range, tidal deformation (amplification, asymmetry) and hydraulic head (water level slope).
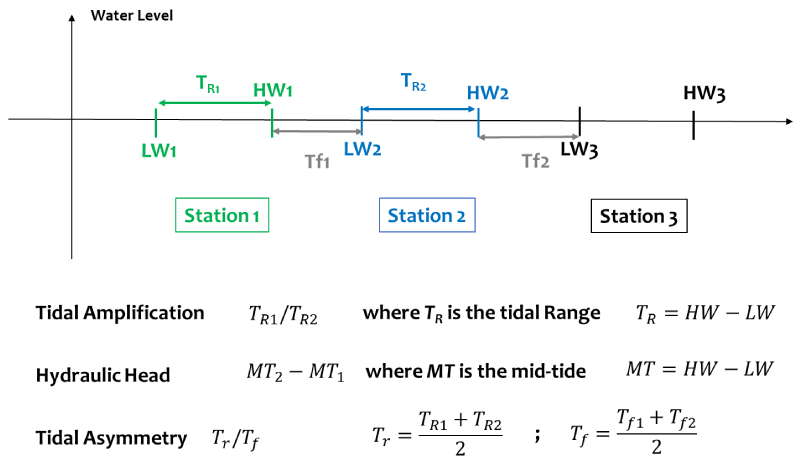
This conceptual approach is based on the determination of the High (HW) and Low (LW) water levels at the different stations for each spring tide cycle. The methods for calculating the tidal range, the hydraulic head, the amplification factor, and the tidal asymmetry are depicted in Figure 2 [24].
Most of the scatters are caused by the spring-neap variation [12]. Therefore, the results of high and low water levels are evaluated over a spring-neap cycle. Similar approaches such as analysis have also been used in earlier studies [8,25].
The astronomical signal at Cherbourg station, where the tidal deformation is negligible, has been used as a reference.
According to Figure 2 and following the methodological approach of Wang, et al. [24], a series of parameters have been conceptually quantified.
- The amplification factor is determined as the ratio between the tidal ranges at the two successive stations. This parameter indicates how the tidal range changes between the two stations in the estuary. Any change in time of this parameter is an indication of changes in the physical conditions in the estuary.
- The hydraulic head (water surface slope) is determined as the difference between the mid-tides at the two successive stations. The direct cause of the hydraulic head is the river discharge. The way in which this parameter depends on the river discharge provides another indication of the physical condition of the river section, especially the hydraulic drag.
- The asymmetry factor is associated with the ratio between the rising and falling periods. This indicator is in particular meaningful under conditions of low river flow. The tide at a station is flood-dominant if this ratio is smaller than one, and ebb-dominant if it is larger than one.
Results
The tidal modulation has been investigated by examining the changes in the different tidal parameters together with the fluvial discharge and the compound flooding events induced by hydrological and marine extremes.
Changes in the harmonic components of tides
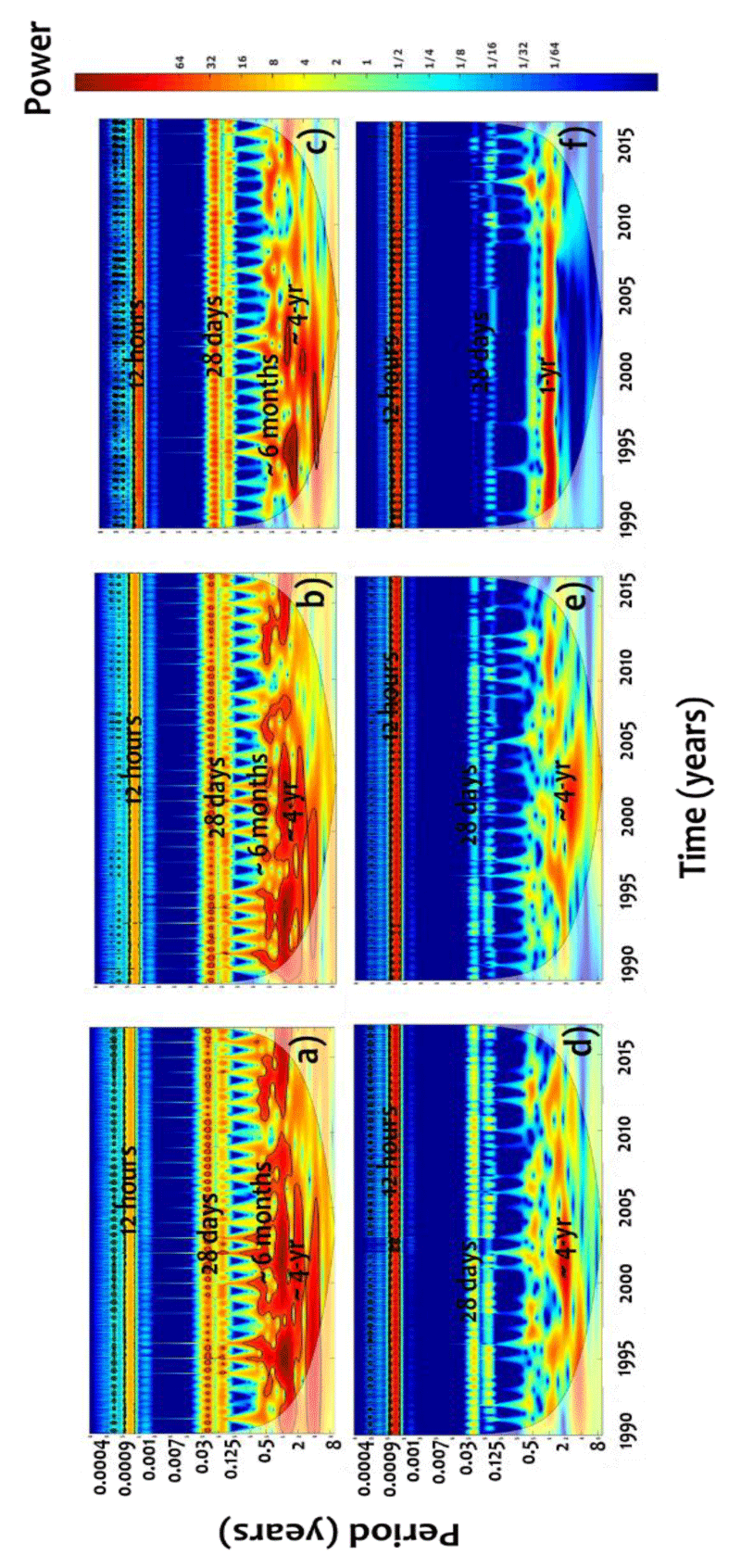
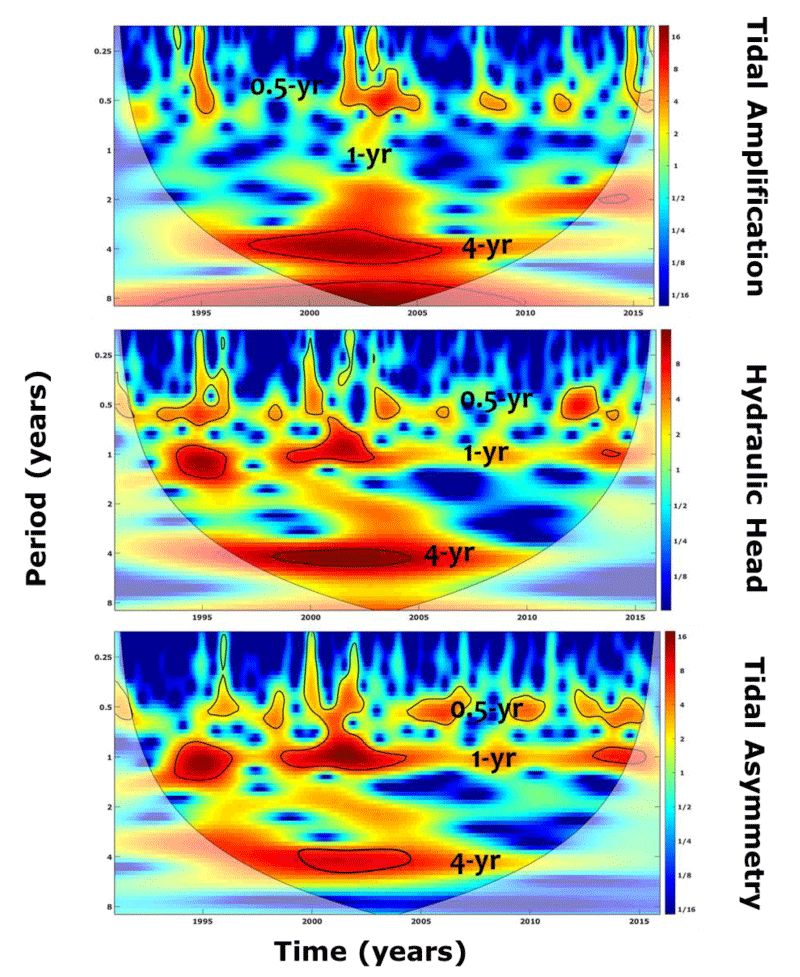
The Continuous Wavelet Transform (CWT) of the tidal signal along the estuary from Rouen to Duclair, Caudebec, Tancarville et Honfleur has been analyzed et compared to the marine station of Cherbourg (Figure 3). In this figure, the distribution of the energy spectrum shows an increasing power (variance) from blue to yellow and red. They highlight the existence of several variabilities (energy) distributed functions of different ranges of frequencies. Overall, we can visually identify three scales of frequencies: ~ 12 hours, 28 days, ~ 6 months (~ 6 months), and ~ 4 years (4 years).
The multi-timescale evolution of the tidal component changes along the estuary. The small scales, described by the neap-spring cycle (~ 28 days), the daily cycle of low-high tide (~ 12 hours), and the interannual scales (~ 4 years) are clearly illustrated at the different sites.
The ~ 4-year mode is significantly manifested at Rouen, Duclair, and Caudebec and relatively less expressed at Tancarville, Honfleur, and then Cherbourg. This mode could be explained by the tidal nodal modulation of 4.35 years.
For the upstream stations (Rouen, Duclair, Caudebec) where the tidal effects are less important, the interannual mode should be related to the long-term changes of tidal transformation (amplification, water surface slope, and tidal asymmetry). The annual mode is clearly illustrated at Cherbourg explaining the altering winter and summer periods at the equinoxes of spring and neap tides [26-28].
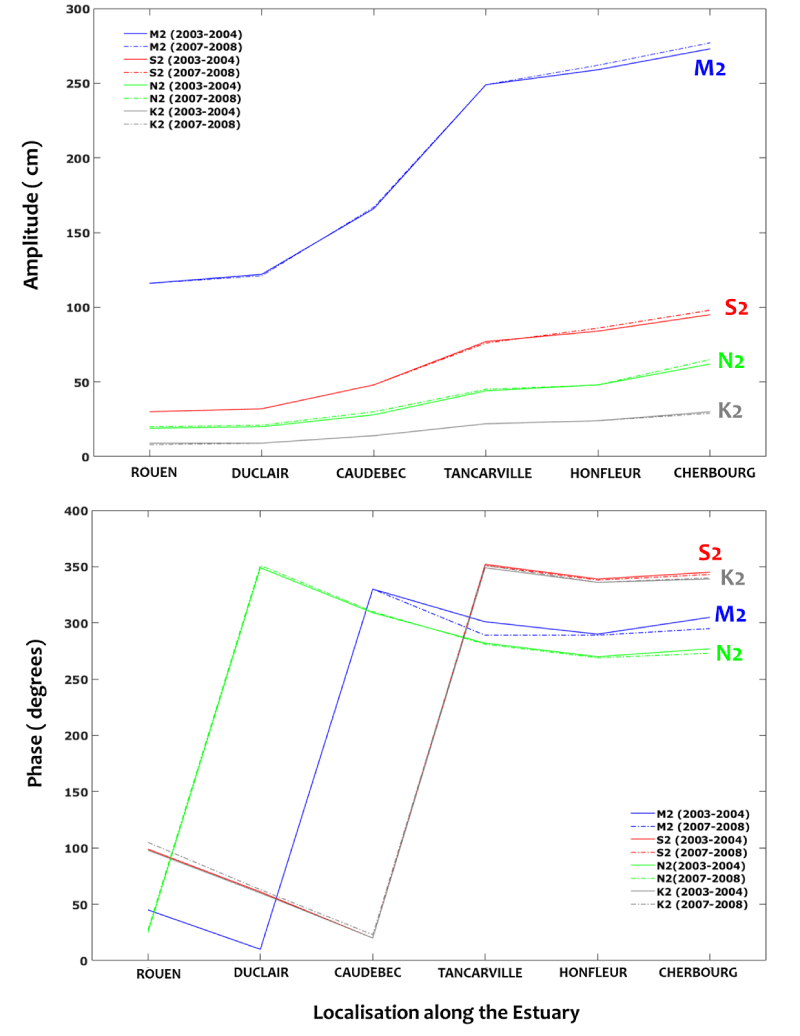
According to the harmonic analyses, the diurnal components of M2, S2, N2, and K2 are the more significant along the Seine Estuary. Their amplitude and phase, quantified from tidal measurements (Figure 4), vary in space, along the estuary, and time between two selected periods, 2003-2004 and 2007-2008.
The amplitude of M2 seems to be significantly important, varying between 120 cm and 230 cm, compared to S2, N2, and K2. The amplitudes of S2, N2, and K2 are lower than 70 cm, 59 cm, and 30 cm, respectively.
The M2 amplitude is approximately two, four, and eight times greater than that of S2, N2, and K2 respectively. The evolution of the overall components has shown an increase in the amplitude from Caudebec to Tancarville and Honfleur. This evolution is more pronounced for the M2 component and tends to be negligible for K2.
Regarding the phase, a shift of an inverse phase is manifested for the different components within the estuary; it is around Rouen for N2, Duclair for M2, and Caudebec for S2 and K2.
Changes in the time of the harmonic components seem to be not significant. The time changes are enhanced for the M2 component in the downstream part of the estuary (close to Honfleur) in terms of amplitude and phase.
Accordingly, the estuarine area between Caudebec and Tancarville is a key zone where the shift of tidal components (in particular for S2 and K2) is clearly manifested. Such a result highlights the changes in the morphological and the geometrical characteristics of the estuary responsible for physical changes in the propagation of tidal waves and their modulation within the Caudebec-Tancarville zone.
Deformation of tidal wave
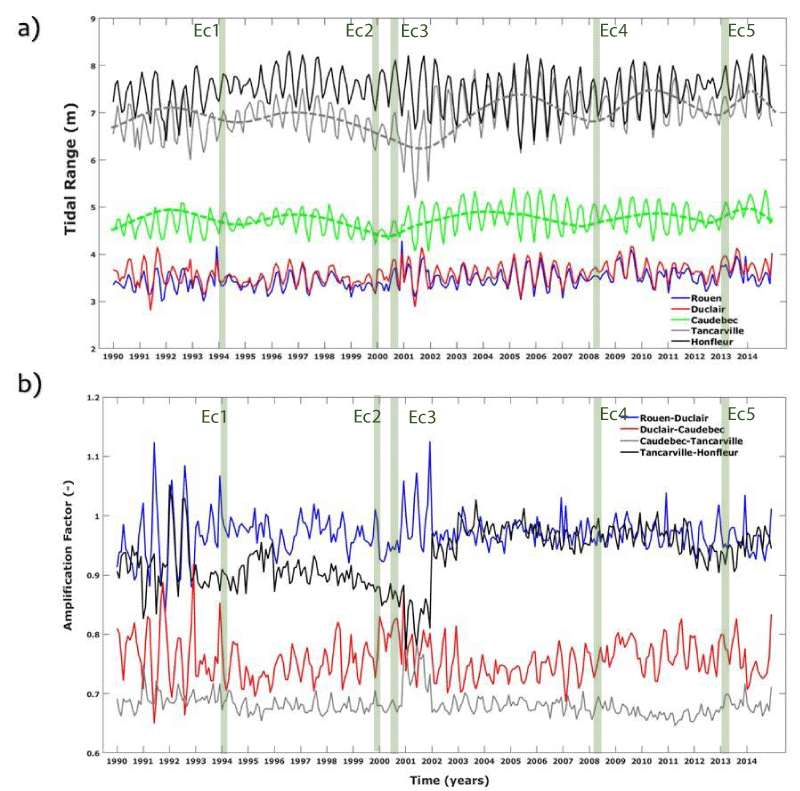
The tidal range increases from the upstream, Rouen, to the downstream station, Honfleur, with a strong transition in Caudebec. The tidal range exhibits altering variations with high and low oscillations during the study period in particular for the lower estuary close to Tancarville and Honfleur. The variation of this range (smoothed line in Figure 5a) shows a series of interannual fluctuations with different time periods. At smaller scales, the annual and seasonal fluctuations are observed and no long-term trend has been identified.
The amplification factor along the estuary, determined between two successive stations, was calculated, defined as the ratio between the tidal ranges at the lower estuary (Honfleur) and the upper estuary (Rouen). Results have shown that this factor is more significant in the upper zone of the Seine estuary (Rouen-Duclair), where high changes induced by the fluvial effects should take place, and decreases in the lower zone close to Tancarville-Honfleur (Figure 5b).
The variation of the amplification factor highlights high changes during both periods 1990-1993 and 2000-2003 which exhibits probably strong fluctuations of the physical conditions in the estuary (e.g., bottom roughness).
The parameters of tidal range and amplification factor, used to characterize the tidal deformation, seem to be strongly correlated with an inverse relation from the higher to the lower estuary (Figure 6).
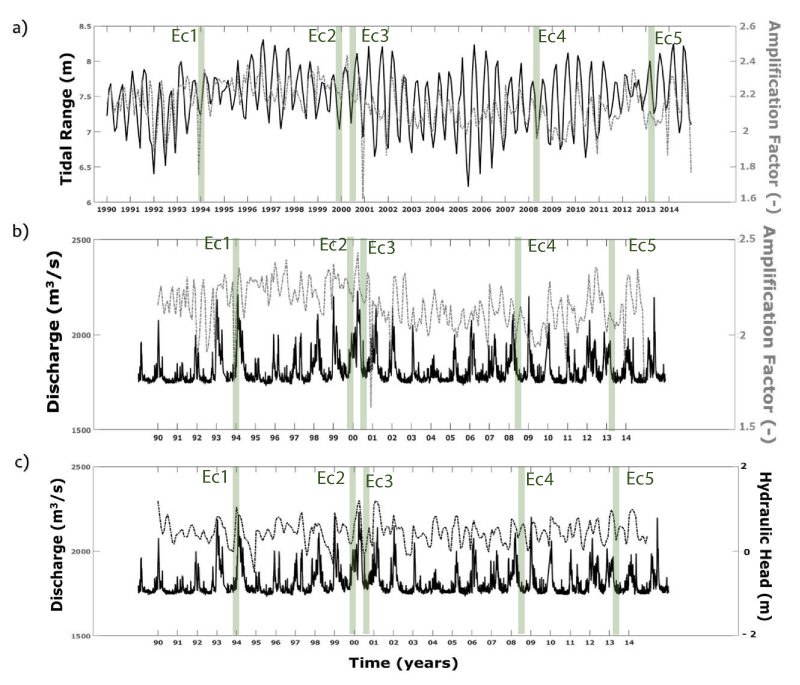
The relationship of the amplification factor Rouen-Honfleur with the discharge at Poissy has been investigated. This relation indicates that weaker tidal amplification and lower tidal range are associated with high river discharge. This inverse correlation is observed during the full period of study.
The water surface slope, tidally averaged along the estuarine system, is described by the hydraulic head calculated as the difference between the mid-tides at Rouen and Honfleur.
Similar to the amplification factor, the hydraulic head seems to be strongly correlated to the river discharge.
The tidal asymmetry is calculated as the ratio between the rising period (Tr) and the falling period (Tf ). A smaller value of the tidal asymmetry reflects that the tide is more flood-dominant.
The tidal asymmetry has been evaluated along the estuary from the upper zone (Rouen-Duclair-Caudebec) to the lower zone (Caudebec-Tancarville-Honfleur). It shows an altering oscillation with small amplitudes less than 0.1 in the upper zone. Higher amplitudes of this factor are observed in the lower zone varying between 1.25 and 1.7. A decreasing trend of the tidal asymmetry is depicted during the period 1995-2000 to reach its minimum in 2001 exhibiting a flood-dominant tide. During the same period, a decrease in the tidal range and the amplification factor are also observed while the hydraulic head is increasing.
Such evolution highlights that the tidal asymmetry is more developed when the river discharge decreases.
The ratio or the difference between the tidal asymmetry in the upper zone of the estuary can be used to characterize the tidal deformation within the river section between Rouen and Caudebec. The ratio in the river section is smaller than 1 and varies between 0.8 and 1; it implies that the vertical tide at Rouen and Duclair is more food-dominant than Caudebec.
For some periods of time (1994, 2001-2002), the ratio is closer to 1 (around 0.98) which implies that the tidal wave is not fully deformed during its propagation within the river section explained by the flood events during such periods
Then, the interannual and seasonal changes in the discharge should be reflected in the amplification factor, the hydraulic head, and the tidal asymmetry parameters.
In the frequency domain (Figure 7), the CWT of the tidal amplification, hydraulic head, and tidal asymmetry shows a multi-timescale variability at seasonal and interannual (~ 4 years) scales. A high energy spectrum seems to be concentrated during the period 2000-2005 at different timescales. Such results are in agreement with those discussed previously related to the multi-timescale variation of the tidal deformation and those demonstrated by the frequency analysis of the tidal signal along the estuary where the interannual scale of ~ 4 years is dominated in the upper zone of the estuary (Rouen, Duclair, Caudebec).
According to the previous works [4,12], the amplification factor increases with a larger tidal range and stronger tidal flow which induce an important frictional dissipation of the tidal wave. For estuaries with high turbidity, the frictional dissipation is generally compensated by the decrease of the hydraulic head when the suspended sediment concentration is higher under a larger tidal range and stronger tidal flow.
On the basis of such results, the upper zone of the Seine estuary shows an inverse behavior to the high turbid estuary. As suggested previously, the tidal range and the amplification factor don’t exhibit any long-term trend and no clear changes in time. This behavior should be explained by an interaction between the high variability of the tidal range and the extreme river discharge. The opposite effect of the river and its resistance is enhanced under higher tidal flow velocity; which increases the water depth and reduces the hydraulic head and the tidal amplification factor in a low turbid estuary.
Tidal wave modulation and flooding
This part addresses the link between the tidal deformation parameters and a series of five historical compound-flooding events, induced simultaneously by extreme floods and storm surges (Ec1-5) produced between 1991 and 2015 and documented in Fisson and Lemoine [29] works: (1) Ec1 is the first one produced on January 1994, (2) Ec2 is the second one produced on December 1999 (Lothar and Martin storms), (3) Ec3 is the third one produced on March 2002; (4) Ec4 is the forth one produced on March 2008; (5) Ec5 is the fifth one produced on February 2013. The magnitude and return period (Re) of each event is described in Table 1.
The historical events, reported in Figures 5 and 6 (green bars), have been investigated together with the different tidal deformation parameters and the fluvial discharge. The overall compound-flooding events Ec2-5, associated with extreme storm surges and fluvial flooding, are highlighted by the peak of tidal range (Figure 5a) and tidal amplification (Figure 5b) at Tancarville and Honfleur, the lower zone of the estuary. The amplification factor is manifested differently between the selected events; it is around 0.75 for the events Ec1, and Ec5, which are associated with storm surges with Re < 2 years. This factor reaches 0.95 for the events Ec2 and Ec3, induced by extreme storm surges with Re > 10 years. Such events seem to be related to a decrease in the hydraulic head parameters (Figure 6).
According to this diagnostic, the link between the historical events of concomitance and the tidal deformation seems to be differently expressed according to the spatial (from up to down estuary) and the energetic characteristics of the compound-flooding, case of Ec1 / Ec5 and Ec2 / Ec3.
Table 1. List of concomitant events produced between 1991 and 2015 [29]: (1) January 1994; (2) December 1999, Lothar and Martin storms; (3) March 2002; (4) March 2008; (5) February 2013. The return period (Re) of each combined event is illustrated [30].
The results provided in this work highlight the physical connections between tidal modulations and harmonic component changes as well as the non-stationary behavior of fluvial discharge. This connection takes a non-linear behavior and contributes to complex variations of water levels [7] which are pronounced under extreme energy conditions of fluvial and marine drivers. Losada, et al. [31] have demonstrated that a high river discharge enhances the friction of tides and their energy attenuation through a non-linear interaction between tides and discharge.
According to this work, the Seine estuary is considered a low turbid system since the larger tidal range causes a lower hydraulic head and smaller amplification factor. The multi-timescale changes of river discharge, from seasonal to inter-annual scales, are also reflected in the tidal signal which depends on the morphology and effective roughness. Similar contributions related to seasonal patterns of tide–river dynamics have been pointed out by Cai, et al. [32]. Their work investigates the tidal damping and residual water level slope in the Yangtze River estuary to quantify the impacts of river discharge on the seasonal behaviour of tide–river dynamics (e.g. tidal damping) using an analytical approach. They have demonstrated, contrary to the common assumption that larger river discharge leads to heavier damping, that tidal damping is slightly reduced with increasing river beyond a critical value of discharge; which is induced by the cumulative effect of the residual water level on the effective friction and channel convergence.
The dependence between river discharge and tides has also been examined by Jalon-Rojas, et al. [33] in the Garonne Tidal River (SW France) by analyzing the evolution of tidal waves over the last six decades in response to natural and human-induced morphological and hydrological changes. Contrary to the Seine, the Gironde estuary is of turbidity maximum induced by tidal pumping. In their works, they have considered the man-activities, including the gravel extraction (1960-1980) responsible for the increasing of tidal range asymmetry and tidal range.
The amplification and deformation of a tidal-river system, case of Scheldt Estuary, have been investigated by Wang, et al. [24] using similar approaches of the tide in the Upper to examine the possible shift from a low turbid and weak amplification regime towards a high turbid and strong amplification regime. They have highlighted the effects of the non-linear interaction between the morphology and the tidal dynamics and the increasing of damping when the tidal amplitude increases even though the flood-dominance decreases.
The evolution of the sedimentation with the intertidal mudflats in the Seine estuary has been examined by Deloffre, et al. [34]. Their works highlight the key role of the non-linear tide-river dynamics and the non-stationary behavior of fluvial, tidal, and surge signals.
In this tide-river environment, the non-stationary dynamics of storm surges and discharge interaction have been addressed by Turki, et al. [30] to evidence the effects of extreme water level variability on the compound flooding events induced by floods and storm surges. This non-stationary behavior of fluvial and surge signals is strongly related to climate oscillations at global scales [26-28,30,35,36].
This work uses the hypothesis of the stationary dynamics of tidal waves. This assumption is valid in deep waters for calculating the oceanic tides; it is limited in shallow waters, case of river-tide environments, where tides are nonstationary.
Conclusion
This research investigates the modulation of tidal waves modulated at different timescales, from the inter-daily to the inert-annual scales, and its relation with coastal flooding in a tide-river environment, case of the Seine estuary (NW France). The t2 idal signal has been analyzed together with the river discharge during 25 years (1990-2015) in Seine Bay, including the estuary and the marine tides at Cherbourg, by the use of a series of spectral and physical approaches. The main results of this research can be summarized as follows:
- The harmonic components of tides in the Seine estuary are mainly dominated by M2, S2, N2, and K2. They increase in amplitude from the upper zone to the lower zone of the estuary (M2=2×S2=4×N2=8×K2).
- The time Changes in both amplitude and phase of the harmonic components are not clearly observed along the estuary (small ones between Tancarville and Honfleur). An important shift of both amplitude (significant increase) and phase (inverse phase) close to Caudebec where changes in physical conditions are important and responsible for the modifications of the tidal propagation.
- The river discharge at Poissy displays a multi-timescale variation from the seasonal to the interannual scales. Such fluctuations are reflected in the tidal deformation (amplification factor, hydraulic head, tidal asymmetry).
- The amplification factor is important in the river section. The river-discharge is inversely correlated to the amplification factor and in phase with the hydraulic head.
- The tidal asymmetry is smaller in the upper estuary and higher in the lower estuary. During the period of 1999-2002, the asymmetry decreased as the amplification factor while the tidal range increased together with the hydraulic head. This behavior exhibits a flood-dominant tide.
- The tidal wave propagation in the river section is determined by two factors: (a) the boundary conditions of the upper and the lower estuary; and (b) the physical conditions of the river section (morphology and effective roughness). Therefore, the development of the tidal amplification, asymmetry, and hydraulic head should be explained according to the tidal propagation.
- The interannual fluctuations of tides are related to tidal deformation for estuarine sites while they are explained by the nodal modulations for marine sites at Cherbourg. The interaction between the river discharge and tides reduces the tidal intrusion, in particular when the discharge increases with an opposite effect. This explains the multi-timescale variability (from seasonal to interannual fluctuations) of the tidal range and the amplification factor. The role of the river discharge is also important; it causes a higher water level increasing the depth and reducing the hydraulic drag.
- Tides in the lower estuary affect the hydraulic drag. Indeed, the larger tidal range causes a higher tidal flow velocity increasing the resistance to the river flow. In the present work, we have demonstrated that a larger tidal range causes a lower hydraulic head and smaller amplification factor. This indicates that the Seine system can be considered a low turbid estuary (muddy estuary).
- The tidal deformation is strongly correlated with the compound-flooding events. This correlation seems to be manifested differently along the estuary from the upper to the lower zone explained by an interaction between the high variability of tidal range and the extreme river discharge. The opposite effect of the river and its resistance is enhanced under higher tidal flow velocity; which increases the water depth and reduces the hydraulic head and the tidal amplification factor in a low turbid estuary.
This work carried out in the framework of the SWOT 3MC research program, gives some insights into the complex behavior of tidal propagation in the Seine estuary and its non-stationary dynamics close to the river effects in response to extreme water variability leading to coastal flooding.
This study is the first to encompass the dynamics of tidal waves in the Seine estuary and its multi-timescale evolution with the fluvial discharge and the compound-flooding events.
This implies that the dynamics of tidal waves, including their asymmetry, are likely to further fluctuate with the expected changes in river flow over the next decades. Future work on the river-tide environment needs to consider the impact of morphology on tidal waves by addressing the time changes in the morphology of intertidal zones.
This work gives some insights into the tidal dynamics in the macro-tidal system, case of the Seine estuary, to be more explored for the next investigations related to the new mission SWOT and the contribution of the imagery as well as altimetry products to improve our understanding of the hydrodynamics in estuarine systems.
The research program CNES-TOSCA ‘SWOT 3MC’ is acknowledged for funding this research related to the future mission of Surface Water and Ocean Topography (SWOT). We also acknowledge the National Navy Hydrographic Service (SHOM), and Rouen Port authorities.
- Dronkers J. Tidal asymmetry and estuarine morphology. Netherlands Journal of Sea Research. 1986. https://doi.org/10.1016/0077-7579(86)90036-0.
- Buschman FA, Hoitink AJF, van der Vegt M, Hoekstra P. Subtidal water level variation controlled by river flow and tides, Water Resource Research. 2009.; 45: W10420. doi:10.1029/2009WR008167.
- Lanzoni S, Seminara G. On tide propagation in convergent estuaries, Journal of Geophysical Research. 1998; 103:30;793–30:812.
- Godin G. The propagation of tides up rivers with special considerations on the upper Saint Lawrence River. Estuarine and Coastal Shelf Sciences. 1999; 48:307–324. https://doi.org/10.1006/ecss.1998.0422
- Rijn VLC. Analytical and numerical analysis of tides and salinities in estuaries; part I: Tidal wave propagation in convergent estuaries, Ocean Dynamics. 2011; 61:1719–1741.
- Tebaldi C, Ranasinghe R, Vousdoukas M. Extreme sea levels at different global warming levels. Nature Climate Change. 2021; 11:746–751. https://doi.org/10.1038/s41558-021-01127-1
- Matte P, Secretan Y, Morin J. Temporal and spatial variability of tidal-fluvial dynamics in the St. Lawrence fluvial estuary: An application of nonstationary tidal harmonic analysis. Journal of Geophysical. Research Ocean. 2014; 119:5724–5744. https://doi.org/10.1002/2014JC009791
- Jay DA, Flinchem EP. Interaction of fluctuating river flow with a barotropic tide: A demonstration of wavelet tidal analysis methods, Journal of Geophysical Research. 1997; 102:5705–5720. https://doi.org/10.1029/96JC00496.
- Godin G. Modification of river tides by the discharge. Journal of Waterway Port Coastal Ocean Engineering. 1985; 111(2):257–274.
- Godin G. Frictional effects in river tides, in Tidal Hydrodynamics. edited by BB Parker. John Wiley, Toronto, Canada. 1991; 379–402
- Cai HY, Savenije HHG, Yang QS, Ou SY, Lei YP. Influence of river discharge and dredging on tidal wave propagation: Modaomen Estuary case, Journal of Hydraulic Engineering. 2012; 138:885–896.
- Wang ZB, Winterwerp JC, He Q. Interaction between suspended sediment and tidal amplification in the Guadalquivir Estuary. In: Ocean Dynamics. 2014; 64:10; 1487–1498.
- Hoitink A, Jay DA. Tidal river dynamics: Implications for deltas. In: Reviews of Geophysics. 2016; 54:1; 240–272.
- Avoine J, Allen GP, Nichols M, Salomon JC, Larsonneur C. Suspended-sediment transport in the Seine estuary, France: effect of man-made modifications on the estuary—shelf sedimentology. Mar. Geol. 1981; 40(1–2):119-137.
- Lesourd S, Lesueur P, Brun-Cottan JC, Garnaud S, Poupinet N. Seasonal variations in the characteristics of superficial sediments in a macrotidal estuary (the Seine inlet, France). Estuarine, Coastal and Shelf Science. 2003; 58(1):3-16.
- Lesourd S, Lesueur P, Fisson C, Dauvin JC. Sediment evolution in the mouth of the Seine estuary (France): A long-term monitoring during the last 150 years. Comptes Rendus Geosciences. 2016; 348:6; 442-450. https://doi.org/10.1016/j.crte.2015.08.001.
- Pugh DT. Tides, surges, and mean sea-level (reprinted with corrections), Chichester, UK. John Wiley & Sons, Ltd. 1996; 486.
- Tsimplis MN, Shaw AGP. Seasonal sea level extremes in the Mediterranean Sea and at the Atlantic European coasts, Nat. Hazards Earth Syst. Sci. 2010; 10:1457–1475, https://doi.org/10.5194/nhess-10-1457-2010, 2010.
- Williams KD, Copsey D, Blockley E, Bodas-Salcedo A, Calvert D, Comer RE. The met office global coupled model 3.0 and 3.1 (GC3 & GC3.1) configurations. Journal of Advances in Modelling Earth Sciences. 2018; 10(2):357–380. doi: 10.1002/2017MS001115
- Foreman M, Crawford WR, Marsden RF. De–tiding: Theory and practice. In Coastal and estuarine studies. 1995;203–239. https://doi.org/10.1029/ce047p0203
- Labat D. Recent advances in wavelet analyses: Part 1. A review of concepts. J. Hydrol. 2005. https://doi.org/10.1016/j.jhydrol.2005.04.003.
- Sang YF. A review on the applications of wavelet transform in hydrology time series analysis. Atmospheric Research. 2013. https://doi.org/10.1016/j.atmosres.2012.11.003
- Torrence C, Compo GP. A Practical Guide to Wavelet Analysis. Bulletin of American Meteorological Society. 1998; 79:61–78. https://doi.org/10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2
- Wang ZB, Vandenbruwaene W, Taal M, Winterwerp H. Amplification and deformation of tidal wave in the Upper Scheldt Estuary. In: Ocean Dynamics. 2019; 69.7:829–839.
- Jay DA, Flinchem EP. A comparison of methods for analysis of tidal records containing multi-scale non-tidal background energy. Cont Shelf Res. 1999; 19:1695–1732.
- Turki I, Laignel B, Chevalier L, Costa S, Massei N. On the Investigation of the Sea-Level Variability in Coastal Zones Using SWOT Satellite Mission: Example of the Eastern English Channel (Western France). IEEE Journal of Selected Topic in Applied Earth Observations and Remote Sensing. 2015; 8:1564–1569. https://doi.org/10.1109/JSTARS.2015.2419693
- Turki I, Massei N, Laignel B, Shafiei H. Effects of Global Climate Oscillations on Inter-monthly to Inter-annual Variability of Sea Levels along the English Channel Coasts (NW France). Oceanologia. 2020a; 62:226–242. https://doi.org/10.1016/j.oceano.2020.01.001
- Turki I, Baulon L, Massei N, Laignel B, Costa S, Fournier M, Maquaire O. A nonstationary analysis for investigating the multiscale variability of extreme surges: case of the English Channel coasts. Natural Hazards and Earth System Sciences. 2020b; DOI: 10.5194/nhess-2020-101.
- Fisson C, Lemoine JP, Gandilhon F, Schaguene J, David E. Référentiel ligne d’eau pour la gestion du risque inondation dans l’estuaire de la Seine : concertation, analyses statistiques et modélisation. La Houille Blanche. 2016; 30–39. https://doi.org/10.1051/lhb/2016005
- Turki EI, Deloffre J, Lecoq N, Gilbert R, Mendoza ET, Laignel B, Salameh E, Barcelo GAD, Fournier M, Massei N. Multi-timescale dynamics of extreme river flood and storm surge interactions in relation with large-scale atmospheric circulation: Case of the Seine estuary, Estuarine, Coastal and Shelf Science. 2023; 287:2023; 108349:ISSN 0272-7714. https://doi.org/10.1016/j.ecss.2023.108349.
- Losada MA, Diez-Minguito M, Reyes-Merlo MA. Tidal‐fluvial interaction in the Guadalquivir River Estuary: Spatial and frequency‐dependent response of currents and water levels. Journal of Geophysical Research Oceans. 2018; 122:847-865. https://doi.org/10.1002/2016JC011984.
- Cai H, Savenije HHG, Garel E, Zhang X, Guo L, Zhang M, Liu F, Yang Q. Seasonal behaviour of tidal damping and residual water level slope in the Yangtze River estuary: identifying the critical position and river discharge for maximum tidal damping, Hydrol. Earth Syst. Sci. 2019; 23:2779–2794. https://doi.org/10.5194/hess-23-2779-2019.
- Jalon-Rojas I, Sottolichio A, Hanquiez V, Fort A, Schmidt S. To what extent multidecadal changes in morphology and fluvial discharge impact tide in a convergent (turbid) tidal river? Journal of Geophysical Research: Oceans. 2018; 123:3241–3258. https://doi.org/10.1002/2017JC013466
- Deloffre J, Verney R, Lafite R, Lesueur P, Lesourd S, Cundy AB. Sedimentation on intertidal mudflats in the lower part of macrotidal estuaries: Sedimentation rhythms and their preservation. Marine Geology. 2007; 241(1–4):19–32. https://doi.org/10.1016.
- Massei N, Dieppois B, Hannah DMM, Lavers DAA, Fossa M, Laignel B, Debret M. Multi-time-scale hydroclimate dynamics of a regional watershed and links to large-scale atmospheric circulation: Application to the Seine river catchment, France. Journal of Hydrology. 2017; 546: 262–275. https://doi.org/10.1016/j.jhydrol.2017.01.008
- Guo L, van der Wegen M, Jay DA, Matte P, Wang ZB, Roelvink D, He Q. River-tide dynamics: Exploration of nonstationary and nonlinear tidal behavior in the Yangtze River estuary. Journal of Geophysical. Research. 2015; 120:3499–3521. https://doi.org/10.1002/2014JC010491

Article Alerts
Subscribe to our articles alerts and stay tuned.
 This work is licensed under a Creative Commons Attribution 4.0 International License.
This work is licensed under a Creative Commons Attribution 4.0 International License.

 Save to Mendeley
Save to Mendeley
